11 / 02 / 2022, 12 / 02 / 2022
(Download Ch-24 in pdf by clicking on the chapter's name above.)
Page nos:- 164-167
We often buy things and then we get money bills of the items. The shopkeeper gives us a bill containing information about what we purchase. Different items purchased by us, their rates and the total amount are mentioned in the bill.
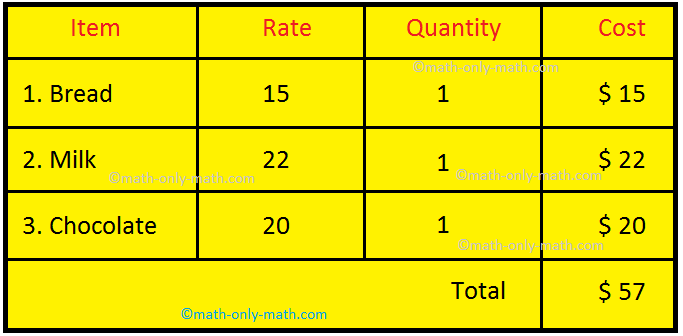
Whenever you go to the shop to buy anything, the shopkeeper gives you bill. The bill consists of all the required details. We usually get a bill at a restaurant, cinema, etc. If you buy 1 bread, 1 packet milk and 1 chocolate, your bill will be shown below.
BILL
Item | Rate | Quantity | Cost |
Bread | 15 | 1 | $ 15 |
Milk | 22 | 1 | $ 22 |
Chocolate | 20 | 1 Total | $ 20 $ 57 |
Now watch the video to help you understand better.
ASSIGNMENTS
Do Chapter-24, Exercise-A full.
31 / 01 / 2022, 07 / 02 / 2022 to 10 / 02 / 2022
Page nos:-160-161
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-23A, full page-161 in ex-bk.
27 / 01 / 2022
Page nos:- 157-159
Temperature
Till now we have learned various types of measurement such length, weight, capacity and time. But none of these measurements can be used to find how hot or cold any object is.
When we touch any hot or cold object, we can make out which is hot and which is cold. But the question here is how much cold or how much hot. At the same time, it is difficult to know the exact level of hotness or coldness by touch because the sense of touch varies from one person to another. To find exact answer, we need some measure of hotness or coldness.
Temperature is the measure of the hotness or coldness of an object with reference to some standard value. The instrument which measures the temperature of body is known as thermometer.
Scales
Each thermometer has a scale. Two different temperature scales that are commonly used are:
Each thermometer has a scale. Two different temperature scales that are commonly used are:
1. The Fahrenheit Scale
The Fahrenheit scale is marked from 32° F to 212° F. 32° F indicates the freezing point of water and 212° F indicates the boiling point of water.
The Fahrenheit scale is marked from 32° F to 212° F. 32° F indicates the freezing point of water and 212° F indicates the boiling point of water.
2. The Celsius Scale
Celsius scale is also called centigrade scale and is marked from 0° C to 100° C. 0° C indicates the freezing point of water and 100° C indicates the boiling point of water.
Comparison of two scales
Conversion of Temperature
When the temperature is given in degree Celsius:
Step 1: Multiply the given temperature in degree by 9
Step 2: Divide the product obtained by 5.
Step 3: Add 32 to the quotient obtained in step 2 to get the temperature in degree Fahrenheit.
Example: 55° C
Here given temperature is 55° C.
To convert into degree Fahrenheit first multiply 55 by 9 and we get product as 495.
Then, divide 495 by 5 and answer we get is 99.
Now, add 32 to 99 and final answer we get is 131.
Therefore, 55° C = 131° F
When the temperature is given in degree Fahrenheit:
Step 1: Subtract 32 from the given temperature in degree
Step 2: Multiply the difference obtained from step 1 by 5.
Step 3: Divide the product obtained from step 2 by 9 to get the temperature in degree Celsius.
Example: 90° F
Here given temperature is 90° F.
To convert into degree Celsius first we need to subtract 32 from 90 and we get 58.
Then, multiply 58 by 5 we get answer as 290.
Now divide 290 by 9 and we get answer as 32.2.
Therefore, 90° F = 32.2° C
Conversion Rule
OR
C = (F – 32) X 5/9
F = 9/5 X C + 32
Clinical Thermometer
A medical thermometer, also known as a clinical thermometer is a thermometer used to measure body temperature. Most of these thermometers have both the two scales, Celsius scale and Fahrenheit scale. The scale runs from 35 degree Celsius to 42 degree Celsius.
The temperature of a healthy human body is approximately 37 °C or 98.6 °F. The tip of the thermometer is inserted into the mouth under the tongue or under the armpit for a minute. Then, the number against the point at which the mercury column stops rising further indicates the body temperature of the person.
Now watch the previous video given on date 24/01/2022.
ASSIGNMENTS
Do Exercise-22A full, page nos-158-159.
24 / 01 / 2022
( Download Ch-22 in pdf by clicking on the chapter name above.)
Page nos:-157-158
ASSIGNMENTS
Study and practice Ch-22, pages 157-158.
20 / 01 / 2022
Page nos:-155-156
1. Find the average of 3.6, 2.7, 4.1, 1.5, and 5.3.
Solution:
Sum of the numbers = 3.6 + 2.7 + 4.1 + 1.5 + 5.3 = 17.2
Number of events = 5.
Average of numbers = 17.2/5 = 3.44
Number of events = 5.
Average of numbers = 17.2/5 = 3.44
2. If the age of 9 students in a team is 12, 13, 11, 12, 13, 12, 11, 12, 12. Then find the average age of students in the team.
Solution:
Given, the age of students are 12, 13, 11, 12, 13, 12, 11, 12, 12.
Average = Sum of ages of all the students/Total number of students
A = (12+13+11+12+13+12+11+12+12)/9
A = 108÷9
A = 12
Hence, the average age of students in a team is 12 years.
3. The average consumption of wheat by a family is 33 kgs in three months. If there are 15 members in the family, find the total consumption for three months.
Solution:
Average = 33 kgs.
No. of members = 15
Total = Average × No. of members.
= 33 × 15
= 495 kg.
Therefore, the total consumption of wheat for 3 months is 495 kg.
Now watch the previous video given on date 17/01/2022.
ASSIGNMENTS
Do Exercise-21A Nos 6-13 , page-156 in ex-bk.
17 / 01 / 2022
(Download Ch-21 in pdf by clicking on the chapter name above.)
Page nos:-154-156
Average means a number which is between the largest and the smallest number.
For example:
Teacher: Children, come one by one and pick up some toffees from the box.
Ron: I have got 8 toffees.
Shelly: I have got 2 toffees.
Mary: I have got 1 toffee.
Teacher: Don’t worry! let me distribute these 24 toffees equally among you.
We divide 24 by 4;
24 ÷ 4 = 6
Thus we observe that on an average each child gets 6 toffees
Or
We can say that the average number of toffees each child gets is 6.
To find the average of a group of numbers, divide the sum of numbers by the total number of events.
Average = Sum of events by total number of events.
Average can be calculated only for similar quantities and not for dissimilar quantities.
Average of height and weight cannot be calculated. It should either be average height of all students or average weight of all students.
The formulas of solving average,
Let us solve some of the examples for the same.
1. The goal scored by a team is 6 matches are 1, 2, 5, 3, 4, 0. Find the average score of the team.
Solution:
Total goal scored by the team = 1 + 2 + 5 + 3 + 4 + 0 = 15
Total number of matches = 6
Therefore, average score of the team = 15/6 = 2.5
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-21A Nos 1-5 , page-156 in ex-bk.
13 / 01 / 2022
ASSIGNMENTS
Do Exercise-20A, Nos 11-25 page no 153 in ex-bk.
10 / 01 / 2022
(Download Ch-20 in pdf by clicking on the chapter's name above.)
Page nos:-148-150
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-20A, Nos 1-10 page nos 152-153 in ex-bk.
******************************************
07 / 12 / 2021
Chapter-14 Profit and Loss
Chapter-15 Line Segments and Angles
Ch-16 Polygons
ASSIGNMENTS
Revise Chapter-14 to 16 all ex's for Formative Assessment-III.
03 / 12 / 2021
Ch-19 Perimeter and Area
Page nos :- 143-147
Area of Square
Definition of Area of a Square
Definition of Area of a Square
The area of a square is the measure of the space or surface occupied by it. It is equal to the product of the length of its two sides. Since the area of a square is the product of its two sides, the unit of the area is given in square units.
Observe the green square shown below. It has occupied 25 squares. Therefore, the area of the square is 25 square units. From the figure, we can observe that the length of each side is 5 units. Therefore, the area of the square is the product of its sides. Area of square = side × side = 5 × 5 = 25 square units.
Area of a Square Formula
The formula for the area of a square when the sides are given, is: Area of a square = Side × Side = S2. Algebraically, the area of a square can be found by squaring the number representing the measure of the side of the square. Now, let us use this formula to find the area of a square of side 7 cm. We know that the area of a square = Side × Side. Substituting the length of side 7 cm, 7 × 7 = 49. Therefore, the area of the given square is 49 cm2.
Find Area of Square When the Side of a Square is Given
Example: Find the area of a square park whose side is 90 ft.
Solution:
Given: Side of the square park = 90ft
We know that,
Area of a square = ft2
Hence, Area of the square park = 902 = 90 × 90 = 8100 ft2
Thus, the area of a square park whose side is 90 ft is 8100 ft2
Let’s discuss how to find length or breadth when area of a rectangle is given.
When we need to find length of a rectangle we need to divide area by breadth.
Length of a rectangle = Area ÷ breadth
ℓ = A ÷ b
Similarly, when we need to find breadth of a rectangle we need to divide area by length.
Breadth of a rectangle = Area ÷ length
b = A ÷ ℓ
Formulas:
For Example:1. Find the length of a rectangle whose breadth is 5 cm and area is 90 sq. cm.Solution:Breadth (b) = 5 cm,Area (A) = 90 sq. cm.Length (ℓ) = Area ÷ breadth= 90 ÷ 5= 18Therefore, length of rectangle = 18 cm.
2. Find the breadth of a rectangle whose length is 200 cm and area is 10 m2.Solution:Length (l) = 200 cm,Area (A) = 10 m2100 cm = 1 m.Length (ℓ) = Area ÷ breadthLength (ℓ) = 200/100 m = 2 m.Breadth (b) = A ÷ ℓ= 10 ÷ 2 m.= 5 m.Therefore, breadth of rectangle = 5 m.Now watch the video given on date 30/11/2021.ASSIGNMENTSDo Exercise-19B, Nos 2-18,page-147 in ex-bk.
30 / 11 / 2021 Ch-19 Perimeter and AreaPage nos:- 143-146
What is Area?In geometry, the area can be defined as the space occupied by a flat shape or the surface of an object.
For Example:
1. Find the length of a rectangle whose breadth is 5 cm and area is 90 sq. cm.
Solution:
Breadth (b) = 5 cm,
Area (A) = 90 sq. cm.
Length (ℓ) = Area ÷ breadth
= 90 ÷ 5
= 18
Therefore, length of rectangle = 18 cm.
2. Find the breadth of a rectangle whose length is 200 cm and area is 10 m2.
Solution:
Length (l) = 200 cm,
Area (A) = 10 m2
100 cm = 1 m.
Length (ℓ) = Area ÷ breadth
Length (ℓ) = 200/100 m = 2 m.
Breadth (b) = A ÷ ℓ
= 10 ÷ 2 m.
= 5 m.
Therefore, breadth of rectangle = 5 m.
Now watch the video given on date 30/11/2021.
ASSIGNMENTS
Do Exercise-19B, Nos 2-18,page-147 in ex-bk.
30 / 11 / 2021
Ch-19 Perimeter and Area
Page nos:- 143-146
What is Area?
In geometry, the area can be defined as the space occupied by a flat shape or the surface of an object.
The area of a figure is the number of unit squares that cover the surface of a closed figure. Area is measured in square units such as square centimteres, square feet, square inches, etc.
The area of the squares below, with unit squares of sides 1 centimeter each, will be measured in square centimeters (cm²).
Here, the area of the shapes below will be measured in square meters (m²) and square inches (in²).
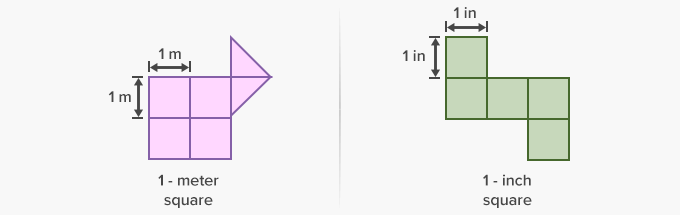
The origin of the word area is from ‘area’ in Latin, meaning a vacant piece of level ground. The origin further led to an irregular derivation of area as ‘a particular amount of space contained within a set of boundaries’.
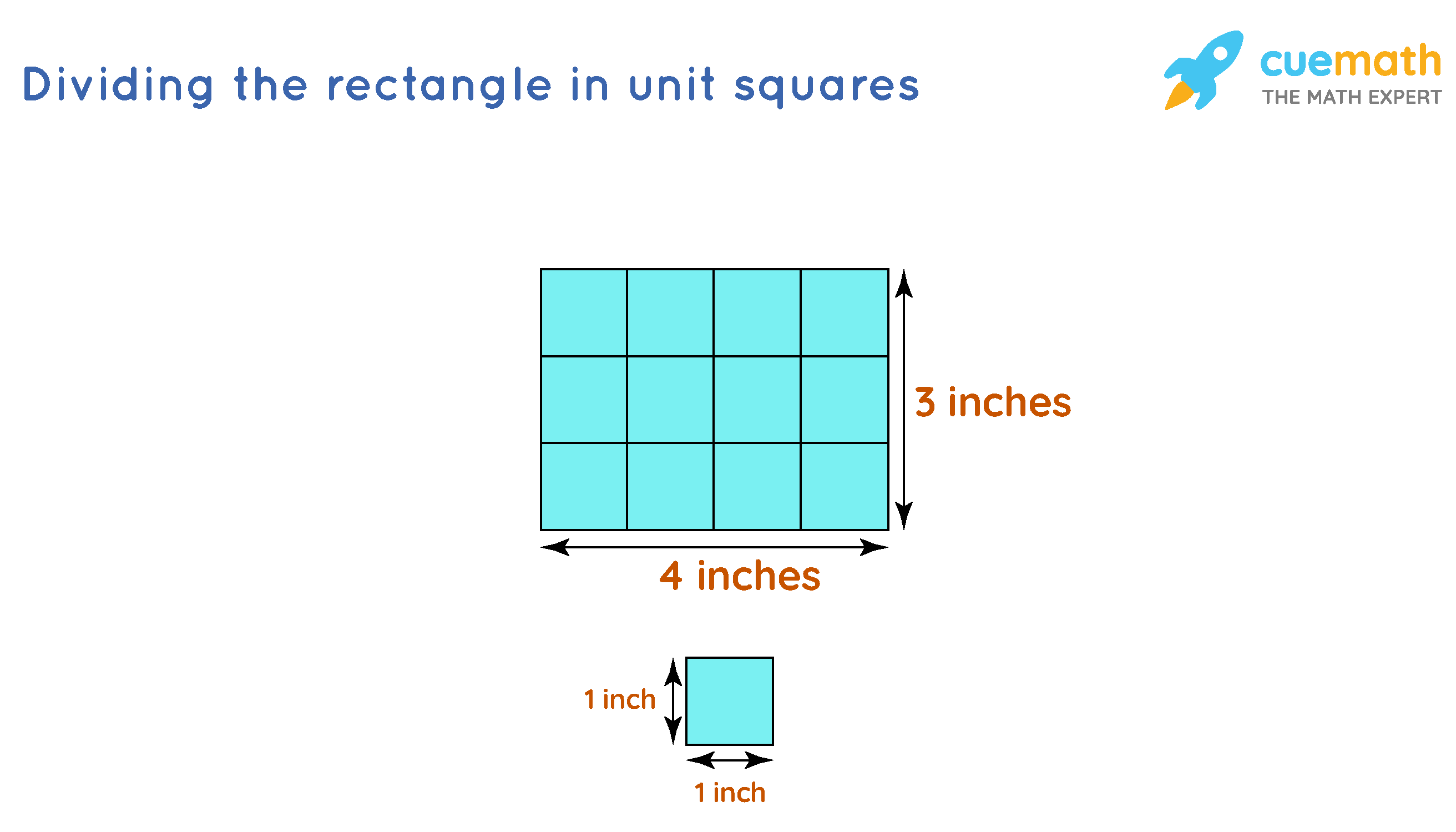
Area of a rectangle Definition: Area occupied by a rectangle within its boundary is called the area of the rectangle.
Let us draw unit squares inside the rectangle. Each unit square is a square of length 1 inch.
Now, count the number of unit squares in the above figure. How many squares can you observe? There are 12 squares in total. We have already learned that area is measured in square units. Since the unit of this rectangle is "inches," the area is measured and written in square inches. Thus, the Area of the above rectangle = 12 square inches.
ASSIGNMENTS
Do Exercise-19B No-1 full, page-146 in ex-bk.
26 / 11 / 2021
( Download Ch-19 in pdf by clicking on the chapter's name above.)
Page nos:-142-143
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-19A Nos 1-15 full, page no-143 in ex-bk.
23 / 11 / 2021
Ch-18 Circle
Page nos:- 139-141
What is Circumference of a Circle?
The circumference of a circle is its boundary or the length of the complete arc of a circle. Let us understand this concept using an example. Consider a circular park as shown below.
If a boy starts running from point 'A' and reaches the same point after taking one complete round of the park, a distance is covered by him. This distance or boundary is called the circumference of the park which is in the shape of a circle. The circumference is the Length of the Boundary.
Circumference of a Circle Definition
The circumference of a circle refers to the measure of its boundary. If we open a circle and measure the boundary just like we measure a straight line, we get the circumference of the circle in terms of units of length like centimeters, meters, or kilometers.
Now let’s learn about the elements that make up circumference. These are the three most important elements of a circle.
- Center: The center is a point that is at a fixed distance from any other point from the circumference.
- Diameter: The diameter is the distance across the circle through the center.
- Radius: The radius of a circle is the distance from the center of a circle to any point on the circumference of the circle.
Circumference of Circle Formula
The circumference formula of a circle can be calculated using the radius 'r' of the circle and the value of 'pi'. Circumference of a circle formula = 2πr. While using this circumference formula, if we do not have the value of the radius, we can find it using the diameter. That is, if the diameter is known, it can be divided by 2 to obtain the value of the radius because of the diameter of a circle = 2 × r. Another way to calculate the circumference of a circle is by using the formula: Circumference = π × Diameter. If we need to calculate the radius or diameter, when the circumference of a circle is given, we use the formula: Radius = Circumference/2π
Illustration: The radius of the circle is 25 units find the circumference of the circle. (Take π = 3.14)
Solution: Given, radius = 25 units
Firstly, we will write the circumference formula and then substitute the value of r (radius) in the same.
Circumference formula = 2πr
C = 2 × π × 25
C = 2 × 3.14 × 25 = 157 units
Therefore, the circumference of a circle is 157 units.
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-18A Nos 5-8 , page no-141 in ex-bk.
16 / 11 / 2021
(Download Ch-18 in pdf by clicking on the chapter's name above.)
Page nos :- 138-139
What is a Circle?
A circle is a round shaped figure that has no corners or edges.
In geometry, a circle can be defined as a closed, two-dimensional curved shape.
A few things around us that are circular in shape are a car tire, a wall clock that tells time, and a lollipop.
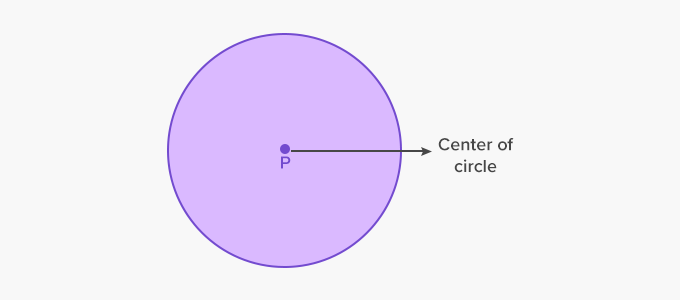
Center of a Circle
The center of a circle is the center point in a circle from which all the distances to the points on the circle are equal. This distance is called the radius of the circle.
Here, point P is the center of the circle.
Semicircle:
A semi-circle is half of a circle, formed by cutting a whole circle along a line segment passing through the center of the circle. This line segment is called the diameter of the circle.
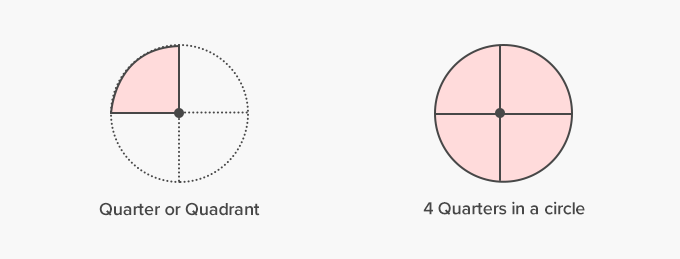
Quarter Circle:
A quarter circle is a quarter of a circle, formed by splitting a circle into 4 equal parts or a semicircle into 2 equal parts.
A quarter circle is also called a quadrant.
How Do You Construct a Circle?
Before constructing a circle, we need to know about the components of a circle.
Circle and its Parts
|
Parts of the circle |
Explanation |
|
Center |
The distance from
the center of the circle to any point on the circle is the same throughout. |
|
Circumference |
The distance
along the circle is called its circumference |
|
Radius |
The distance from
the center to any point on the circle is the radius of the circle. |
|
Diameter |
Is the biggest
chord and is twice the radius. |
|
Chord |
A chord is a line
segment that connects any two points on the circumference of the circle. |
|
Arc |
A part of the
circumference is called an arc. |
|
Segment |
The region
subtended between an arc and a chord is the segment. |
|
Sector |
The region
subtended between two radii and an arc is the sector. |
Construction of a Circle
- Mark a center point.
- Spread the compass according to the convenience or given radius.
- Measure the distance between the tips of the compass and the pencil using the ruler to align with the desired radius.
- Place the metal tip on the center point.
- Keeping the metal tip constant at the center point, rotate the pencil.
- You get a circle!
Thus a circle is constructed.
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-18A Nos 1-4 , page no-141 in ex-bk.
12 / 11 / 2021
Chapter-17 Triangle
Page nos:-134-136
Now watch the video given below.
ASSIGNMENTS
Do Exercise-17A Nos 11-16, pg-137 in ex-bk.
02 / 11 / 2021
(Download Ch-17 in pdf by clicking on the chapter's name above.)
Page nos:-132-134
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-17A Nos 1-10, pg-137 in ex-bk.
29 / 10 / 2021
Chapter-16 Polygon
Page nos:-130-131
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Chapter-16, Exercise-A full.
26 / 10 / 2021
Ch-15 Line Segments and Angles
Page nos:- 124-127
Pairs of angles are discussed here in this lesson.
1. Complementary Angles:
Two angles whose sum is 90° (that is, one right angle) are called complementary angles and one is called the complement of the other.
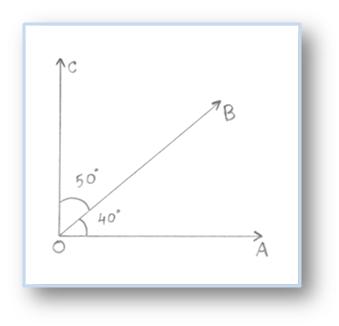
Here, ∠AOB = 40° and ∠BOC = 50°
Therefore, ∠AOB + ∠BOC = 90°
Here, ∠AOB and ∠BOC are called complementary angles.
∠AOB is complement of ∠BOC and ∠BOC is complement of ∠AOB.
For Example:
(i) Angles of measure 60° and 30° are complementary angles because 60° + 30° = 90°
Thus, the complementary angle of 60° is the angle measure 30°. The complementary angle angle of 30° is the angle of measure 60°.
Working rule: To find the complementary angle of a given angle subtract the measure of an angle from 90°.
So, the complementary angle = 90° - the given angle.
2. Supplementary Angles:
Two angles whose sum is 180° (that is, one straight angle) are called supplementary angles and one is called the supplement of the other.
Here, ∠PQR = 50° and ∠RQS = 130°
PQR + ∠RQS = 180° Hence, ∠PQR and ∠RQS are called supplementary angles and ∠PQR is supplement of ∠RQS and ∠RQS is supplement of ∠PQR.
For Example:
(i) Angles of measure 100° and 80° are supplementary angles because 100° + 80° = 180°.
Thus the supplementary angle of 80° is the angle of measure 100°.
Thus the supplementary angle of 80° is the angle of measure 100°.
Working rule: To find the supplementary angle of a given angle, subtract the measure of angle from 180°.
So, the supplementary angle = 180° - the given angle.
3. Adjacent Angles:
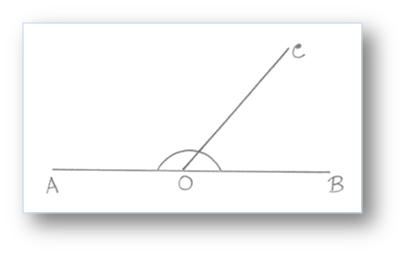
Two non – overlapping angles are said to be adjacent angles if they have:
(a) a common vertex
(b) a common arm
(c) other two arms lying on opposite side of this common arm, so that their interiors do not overlap.
The above given figure, ∠AOB and ∠BOC are non – overlapping, have OB as the common arm and O as the common vertex. The other arms OC and OA of the angles ∠BOC and ∠AOB are an opposite sides, of the common arm OB.
Hence, the arm ∠AOB and ∠BOC form a pair of adjacent angles.
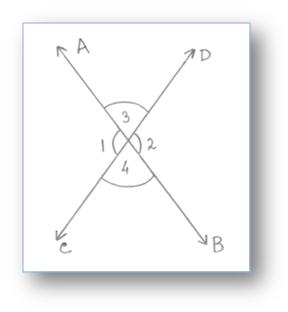
4. Vertically Opposite Angles:
Two angles formed by two intersecting lines having no common arm are called vertically opposite angles.
In the above given figure, two lines and intersect each other at a point O.
They form four angles ∠AOC, ∠COB, ∠BOD and ∠AOD in which ∠AOC and ∠BOD are vertically opposite angles. ∠COB and ∠AOD are vertically opposite angle.
5. Linear Pair:
Two adjacent angles are said to form a linear pair if their sum is 180°.
These are the pairs of angles in geometry.
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Chapter-15, Exercise-A Nos 7 to 15, page nos 128-129 in ex-bk.
22 / 10 / 2021
(Download Ch-15 in pdf by clicking on the chapter's name above.)
Page nos :-119-124
In geometry, a point is a location represented by a dot. A point does not have any length, width, shape or size, it only has a position. When two distinct points are connected they form a line.
What is a Point and a Line?
The concept of points and lines is important to understand geometry figures. With the help of points, we can label and identify the geometry figures and with the help of lines, we can draw the figures.
Point
A point is defined as a location in any space and is represented by a dot (.). It does not have any length, height, shape, or size. It marks the beginning to draw any figure or shape and is labelled with capital letters.
Line
A series of points connected by a straight path is defined as a line. A line is usually defined by two points. It can be marked with a single letter in the lower case or by two capital letters. A line has no thickness and can extend indefinitely in both directions. The length of a line is undefined and it can have infinite numbers of points. Observe the following figure to know the difference between a point and a line.
Distinction between a line segment, a ray and a line
Measurement of a Line Segment
Here we will learn to measure the length of a line-segment.
Let there be a line-segment AB.
We have to measure its length.
Let there be a line-segment AB.
We have to measure its length.
The scale is placed along the line-segment putting its zero (0) mark at A. We see the end B is at the 3 cm mark of the scale. So the length of the line-segment AB = 3 cm.
Angles
Angles are formed when two lines intersect at a point. The measure of the “opening” between these two lines is called an “Angle”. It is denoted by using the symbol ∠. Angles are usually measured in degrees and radians, which is a measure of circularity or rotation. Angles are a part of our day-to-day life. Engineers and architects use angles for the design of roads, buildings, and sporting facilities. In the above image, we can see a surveyor using a Theodolite at a construction site to measure the angle. Let’s see, how many of you like sports! Have you ever watched a game of football? Did you observe where the players take the corner kick from? Well, the point at which the lines intersect is what forms an angle!
Parts of an Angle
In-plane geometry, an angle is formed when two rays are joined at their endpoints. There are different parts of the angle-
1. Two rays, which are called the sides of the angle. Look at the given image, sides OA and OB are sides of the angle AOB.
The common protractor is a simple measuring instrument that is typically semicircle in shape with markings from 0° to 180° on it. We use a protractor to measure angles. Architects and designers use a more precise protractor called an angle protractor tool which gives more accurate measures.
What is a Protractor?
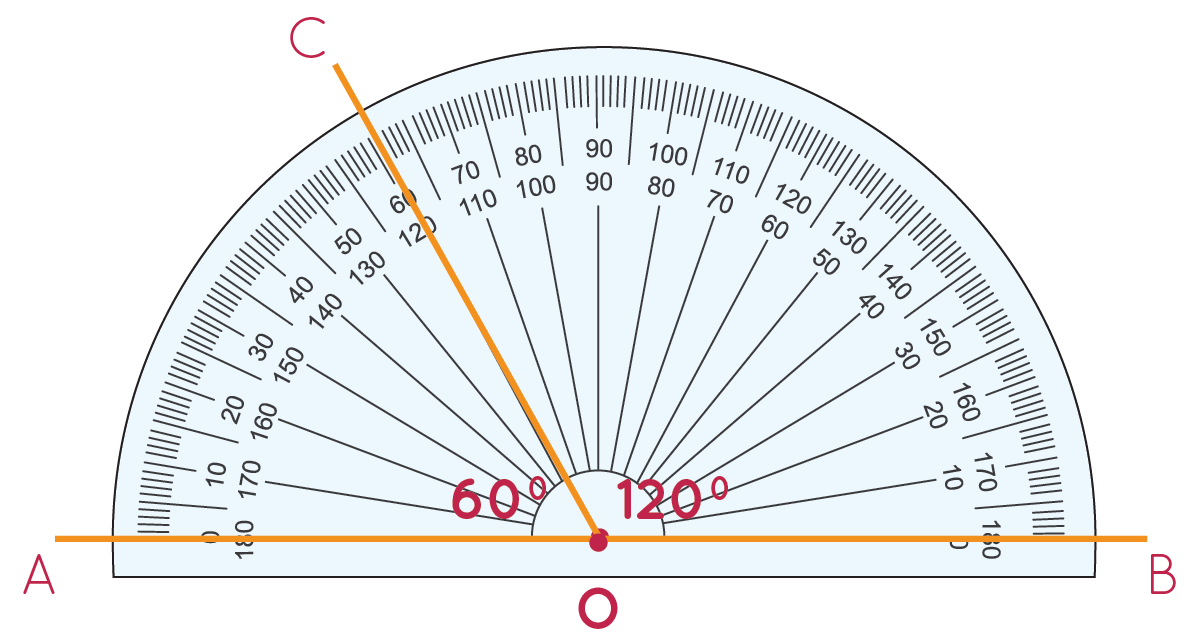
Protractor in maths is considered an important measuring instrument in the geometry box. The protractor tool helps us measure an angle in degrees. A radian scale protractor measures an angle in radians. If you observe closely, a protractor tool has degrees marked from 0 to 180 from left to right in the outer edge and from 180 to 0 in the inner part.
- The inner readings and outer reading supplements each other. i.e, they add up to 180°.
- If the angle to be measured is at the left part of the protractor, we need to use the outer reading of the protractor. ∠AOC = 60°. See in the picture below.
- If the angle to be measured is at the right part of the protractor, we need to use the inner readings of the protractor. ∠BOC = 120°. See in the picture below.
Draw and Measure Angles Using Protractor
In this section you are going to learn how to draw and measure angles using a protractor which is very important for us to know to have a complete understanding of protractor. Let us see how to draw an angle of 30º using a protractor.
- Draw a baseline AB.
- Mark the point O and place the center of the protractor at O.
- Align the baseline of the protractor with the line OB.
- In the inner readings, look for 30º and mark it as point C.
- Now using a scale, join O and C.
∠COB = 30°
Types of Angles based on degree measures.
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Chapter-15, Exercise - A Nos 1-6 pages 127-128 in ex-bk.
08 / 10 / 2021
Chapter- 14 Profit and Loss
Page nos:- 117-118
Profit Percent (P%): It is the percentage of profit on the cost price.
Loss Percent (L%): It is the percentage of loss on the cost price.
Example 1: Dia bought rice bag rupees 500 per bag. Due to spoilage, she had to sold them for rupees 450 per bag. Find the gain or loss%.
Solution:
Here, C.P = Rupees 500 per bag
S.P = Rupees 450 per bag
As S.P < C.P, Therefore Dia suffer a loss.
Loss = C.P – S.P = 500 – 450 = Rupees 50 per bag
Loss% = Loss/C.P X 100 = 50/150 X 100 = 33.33%
Example 2: Mr Ravi bought a washing machine for rupees 15,000 and sold it for rupees 17,000. Find his profit or loss percent.
Solution:
Here, C.P = Rupees 15,000
S.P = Rupees 17,000
As S.P > C.P, therefore Ravi made a profit.
Profit = S.P – C.P = 17,000 – 15,000 = Rupees 2000
Profit % = Profit/C.P X 100 = 2,000/15,000 X 100 = 13.33%
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-14B Nos 1,2,4,6,8,10,12,14,16,18 and 20 page-118 in ex-bk
05 / 10 / 2021
(Download Ch-14 in pdf by clicking on the chapter's name above.)
Page nos :- 115-116
Introduction
Every company and business works on the fundamental concept of profit and loss. It is very important to familiarize yourself with profit and loss, not only to run a business or company but also to keep an account of your own expenditure. Money is actually a tricky concept to explain to kids without giving them an opportunity to get hands-on experience. Parents often take their kids to the supermarket to make them learn about the price marked on every good and the calculation of total price. Later, kids come across the concept of discount on the cost price and the concept of comparing prices before purchasing. Comparing prices is also a form of profit and loss as you learn to save money by buying the same good at a comparatively lesser price.
Terms Related to Profit and Loss
We have come across the word profit and loss many times. Profit stands for gain, advantage or benefits whereas loss is the opposite of profit that involves expenditure as compared to gain.
Cost Price (CP): It is the amount at which a product is purchased. Sometimes it also includes overhead expenses, transportation cost, etc. For example, you bought a refrigerator at Rs 10,000 and spent Rs 2000 for transportation and Rs 500 for set up. So the total cost price is the sum of all the expenditure done, that is, Rs 12,500.
Selling Price (SP): It is the amount at which a product is sold. It may be more than, equal to or less than the cost price of the product. For example, if a shopkeeper bought a chair at Rs 500 and sold it at Rs 600, then the cost price of the chair is Rs 500 and the selling price of the chair is Rs 600.
Profit (P): If a product is sold at a price more than its cost price then the seller makes a profit. For example, a plot was purchased at Rs 50,000 and three years later it was sold at Rs 1,50,000 then there is a profit of 1 lakh.
Loss (L): If a product is sold at a price less than its cost price then the seller makes a loss.
For example, a phone is bought at Rs 20,000 and a year later it was sold for Rs 12,000 then the seller made a loss of Rs 8000.
For example, a phone is bought at Rs 20,000 and a year later it was sold for Rs 12,000 then the seller made a loss of Rs 8000.
Solved Problems
Q. 1: Suppose a shopkeeper has bought 1 kg of apples for 100 rs. And sold it for Rs. 120 per kg. How much is the profit gained by him?
Solution:
Cost Price for apples is 100 rs.
Selling Price for apples is 120 rs.
Then profit gained by shopkeeper is ; P = SP – CP
P = 120 – 100 = Rs. 20/-
Example 2: Ravi has a Alto car worth rupees 2,50,000 and he wants to sell it at profit of rupees 50,000. What should car selling price be?
Solution:
Here, C.P = 2,50,000
Profit = 50,000
S.P = C.P + Profit
= 2,50,000 + 50,000
= Rupees 3,00,000
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-14A full in ex-bk.
14 / 09 / 2021
REVISION
Chapter- 8 Measures of Length, Mass and Capacity ( Decimal System )
Chapter-9 Simplification- BODMAS Rule
Revise Chapters- 8 and 9 all exercises.
07 / 09 / 2021
Ch-10
REVISION
Ch-11 UNITARY METHOD
Ch-12
Revise Chapters-10,11,12 and 13.
03 / 09 / 2021
(Download Ch:13 in pdf by clicking on the chapter's name above.)
Percentage
Very often we come across symbol %. A fraction with denominator 100 is called percentage and is represented by the symbol %. Percent means “per hundred”. 20% means 20 per 100. Percent always compares a quantity to 100 only.
A percent can be written as a fraction or a decimal.
Thus, 20 percent or 20% (as percentage)
Thus, 20 percent or 20% (as percentage)
Or 20/100 (as fraction)
Or 0.20 (as decimal)
Conversion
To convert a % into fraction, divide the given number by 100 and reduce it to its lowest term.
To convert a % into fraction, divide the given number by 100 and reduce it to its lowest term.
To convert a fraction into a percentage (%), multiply the fraction by 100.
To find the percent of a given number
To find what percent is one number of another number.
To calculate a number when its percentage is known
Example: In an examination, Suresh got 200 questions. If he had attempted 80% of the questions then calculate how many questions did he attempt?
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-13A Nos 1-7 ( a-e ), pages 111-112 and Exercise-13B Nos 1,3,5,7,9,11,13,15,17,19 and 21 pages 113-114 in ex-bk.
31 / 08 / 2021
(Download Ch:12 in pdf by clicking on the chapter's name above.)
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-12A Nos 1-6 ( a,b,c,d ) , Nos 7,9,11,13 and 14 pages 107-108 in ex-bk.
27 / 08 / 2021
(Download Ch:10 in pdf by clicking on the chapter's name above.)
We will learn about Roman Numeration and its rules. We know that there are seven basic Roman Numerals. They are I, V, X, L, C, D and M. These numerals stand for the number 1, 5, 10, 50, 100, 500 and 1000 respectively. We already learned about the numerals I, V, X, L and C and now we will learn about the remaining two numerals.
There is another symbol ‘─’ which is called bar. If bar is place over a numeral, it is multiplied by 1000. Thus, V and XII stand for 5000 and 12000 respectively.
(Download Ch:11 in pdf by clicking on the chapter name above.)
In unitary method we will learn how to find the value of a unit from the value of a multiple and the value of a multiple from the value of a unit.
When we go to the market to buy any article, we ask the shopkeeper to tell the price of the article. This is called unit price. We calculate the price of number of articles, we want to buy, with the help of this unit price. Sometimes, we calculate unit price when the price of a multiple is given. The method to calculate the price of the required articles is called unitary method.
Generally, first we find the value of one article from the value of a multiple and then we find the value of the desired number of articles from the value of one. Usually this method involves the operations of multiplication and division both.
Let us consider some examples on unitary method:
1. 2 balls cost Rs 8. Find the cost of 3 balls.
Cost of 2 balls = Rs 8
Cost of 1 ball = Rs 8 ÷ 2 = Rs 4
Cost of 3 balls = Rs 4 × 3 = Rs 12
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise 10A Nos 1-6 page-100 and Exercise-11A Nos 1,3,5,7,9,11,13,15,17,19 and 20 pages-103-104 in ex-bk.
24 / 08 / 2021
(Download Ch-9 in pdf by clicking on the chapter's name above.)
Page nos:- 92-93
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-9A, Nos 1,3,5,7,9,11,13,15,17,19,21 and 23 pages 93 and 94 in ex-bk.
10 / 08 / 2021
Ch: 8 Measures of Length, Mass and Capacity (Decimal System)
Page nos: 88-90
Example:1
Page nos: 88-90
Example:1
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-8B Nos 1,3,5,7,9,11,13,15,17,19,21 and 23 page 89 and Exercise-8C Nos 2,4,6,8,10,12,14,16,18 and 20 page 91 in ex-bk.
06 / 08 / 2021
Ch: 8 Measures of Length,Mass and Capacity (Decimal System)
Ch: 8 Measures of Length,Mass and Capacity (Decimal System)
(Download Ch:8 in pdf by clicking on the chapter's name above.)
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-8A Nos 1-7 and Nos 8-20 (a,c) pages 87-88 in ex-bk.
03 / 08 / 2021
Ch: 7 Decimal Fractions
Page nos:- 80-83
Page nos:- 80-83
Division of Decimal Numbers
In class IV, we have learnt division of decimal numbers by 10, 100, 1000 etc. Here, we will learn division of decimal number by whole number and decimal number.
Division of Decimal Number by 10, 100, 1000, etc.
When we division a decimal number by 10, 100, 1000, etc., the decimal point is shifted to left depending on the number of zeros present. For example, if a decimal number is divided by 10 then the result will remain same, but the decimal point will be shifted to the left by one place. Similarly, if a decimal number is divided by 100 then the decimal point will be shifted to the left by two places.
When we division a decimal number by 10, 100, 1000, etc., the decimal point is shifted to left depending on the number of zeros present. For example, if a decimal number is divided by 10 then the result will remain same, but the decimal point will be shifted to the left by one place. Similarly, if a decimal number is divided by 100 then the decimal point will be shifted to the left by two places.
Example 1. Divide 8.7 by 10.
Solution.
Example 2. Divide 134.26 by 100.
Solution.
Division of Decimal Number by Whole Number
When we divide decimal number by a whole number, as soon as the tenths digit comes down from the dividend, a decimal point is placed in the quotient. Let’s see some examples.
Example 1. Divide 27.5 by 5.
Solution.
So, the answer is 5.5.
Example 2. Divide 64.1 by 2.
Solution.
So, the answer is 32.05.
Division of Decimal Number by Decimal Number
When we divide a decimal number by another decimal number, first we must convert the divisor into a whole number and then divide the dividend decimal number by the whole number. Let’s have a look at some examples.
Example 1. Divide 230.22 by 0.3.
Solution. First, we must convert the divisor 0.3 into a whole number.
So, the answer is 767.4.
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-7G Nos 1-4 (a,c,e,g,i,k,l) pages 82-83 in ex-bk.
30 / 07 / 2021
Ch: 7 Decimal Fraction
Page nos:- 77-79
Multiplication of a decimal fraction by a decimal fraction
The rules to multiply a decimal by a decimal are:
(i) Remove the decimals of the two numbers and then take the two numbers as whole numbers and multiply
(ii) In the product, place the decimal point after leaving digits equal to the total number of decimal places in both numbers.
(iii) Counting must always be done from the units place of the product.
Let us consider some of the following examples on multiplication of a decimal number by a decimal number.
Example1: Find the product of 1.2 × 1.2
First we will perform the multiplication ignoring the decimal points in multiplicant and multiplier.
Since 12 × 12 = 144
Now place the decimal point in the product to give as many decimal places in the product as there are in the multiplicant and the multiplier together.
Therefore, 1.2 × 1.2 = 1.44
Example 2 :
PROPERTIES OF MULTIPLICATION OF DECIMALS
1. The product of a decimal and a whole number multiplied in any order remains the same.
For Example:
(i) 0.9 × 12 = 12 × 0.9 = 10.8
2. The product of two decimal numbers remains the same, even if the order is changed.
For Example:
(i) 2.5 × 3.5 = 3.5 × 2.5 = 8.75
3. The product of a decimal fraction and 1 is the decimal fraction itself.
For Example:
(i) 1.092 × 1 = 1.092
4. The product of a decimal fraction and zero is zero.
For Example:
(i) 891.56 × 0 = 0
5. While performing multiplication in decimals, the numbers can be taken in any order and the product remains the same.
For Example:
(i) 1.02 × (11.2 × 2.3) = 1.02 × 25.76 = 26.2752 | (1.02 × 2.3) × 11.2 = 2.346 × 11.2 = 26.2752 |
Therefore, 1.02 × (11.2 × 2.3) = (1.02 × 2.3) × 11.2
Now watch the previous video given on date (27/07/2021) to help you understand better.
ASSIGNMENTS
Do Exercise 7E Nos 1,3,5,7,9,11,13,15,17,19,21,23,25 and 27 pages 78-79 and do Exercise-7F full pages 79-80.
27 / 07 / 2021
Ch:7 Decimal Fraction
Page nos:-74-76
MULTIPLICATION OF DECIMAL FRACTIONS
MULTIPLICATION OF DECIMAL FRACTIONS BY 10,100,1000,10000 etc .
( POWERS OF 10 )
MULTIPLICATION OF A DECIMAL FRACTION BY A WHOLE NUMBER
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-7C Nos 2,4,6,8,10,12,14 and 16 page 75 and Exercise-7D Nos 1,3,5,7,11,13,15,17,19,21 and 23 page 77.
23 / 07 / 2021
Ch:7 Decimal Fraction
Page nos:-72-73
Ch:7 Decimal Fraction
Page nos:-72-73
Adding and Subtracting Decimals
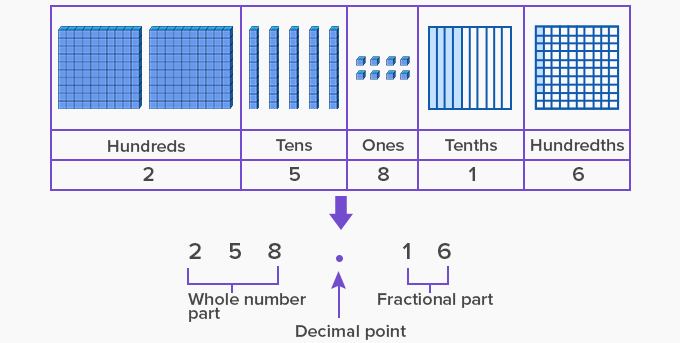
Decimal number
A decimal number is a fraction is a power of 10. For example, the fraction 4⁄10 can be written in decimal form as 0.4 .
The dot is called the decimal point.
The number to the right of the decimal point denotes the numerator of the fraction, that is, the fractional part.
The number to the left of the decimal point denotes the whole number part of the fraction.
For example, 4 3⁄10 is expressed as 4.3, where 4 is the whole number part and 0.3 is the fractional part.
The decimal point separates the whole number part from the fractional part.
Steps to add or subtract Decimals:
Convert decimals to like decimals. (Decimals that have the same number of digits after the decimal point are like decimals).
Write the decimals one below the other as per the places of the digits.
Add or subtract starting from the rightmost digit and moving towards the leftmost digit.
Place the decimal point under the decimal point in the answer.
Example: Add 23.45; 13.101 and 345.5
1. Convert to like decimals: The highest decimal place is 3, so we add zeros in other numbers and get 3 decimal places in them too.
13.101
23.45 = 23.450
345.5 = 345.500
2. Line up the decimals:
3. Add:
4. Place decimal in answer:
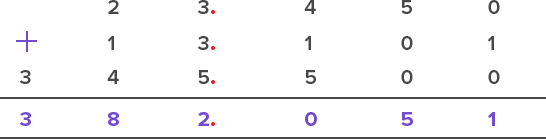
Example: Kylie had 25 m of ribbon. She uses 8 m and 13 cm to decorate a skirt. How much ribbon is remaining with Kylie?
Solution:
Length of ribbon Kylie had = 25 m = 25.00
Length of ribbon used by Kylie = 8 m 13 cm = 8.13
The remaining length of ribbon = 25.00 – 8.13
= 16.87
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise- 7B Nos 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35 and 37 page nos 73-74 in ex-bk.
20 / 07 / 2021
Ch: 7 Decimal Fraction
Ch: 7 Decimal Fraction
(Download Ch:7 in pdf by clicking on the chapter's name above.)
Page nos:-65-70
What
When you place zeros to the right of a decimal, its value stays the same. These zeros are called trailing
zeros,
and they do not change the value of the number.0.8
=
0.80
=
0.800
Now watch the video to help you understand better.
ASSIGNMENTS
Study and practice Ch:7 Decimal Fractions pages 65-70 and do Exercise-7A Nos 1 to 9 ( a,b,c,d ) + Nos 11,13,15,17,19,21 and No-22 ( a,c,e ) page nos 70-72 in ex-bk.
16 / 07 / 2021
Ch:6 Fractional Numbers
Page nos:- 60-62
Word Problems
Reciprocal of a Fraction
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-6G Nos 1,3,5,7,8,9 and 10 page nos 60-61 and Exercise-6H full page no 62 in ex-bk.
13 / 07 / 2021
Ch:6 Fractional Numbers
Page nos :- 56-59
Ch:6 Fractional Numbers
Page nos :- 56-59
MULTIPLICATION OF A FRACTIONAL NUMBER BY A FRACTIONAL NUMBER
When we multiply a fractional number, multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction. The first product is the numerator and the second product is the denominator of the required product.
When we multiply a fractional number, multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction. The first product is the numerator and the second product is the denominator of the required product.
The following rules are given below for the multiplication of a fractional number by a fractional number:
(a) Change mixed fraction into improper fraction.
(b) Product of two fractions = (Product of numerators)/(Product of denominators).
(c) Reduce numerator and denominator to the lowest terms.
(d) The answer should be a whole number, a mixed fraction or a proper fraction and never an improper fraction.
For Example:-
Properties of Multiplication of Fractions
Property 4 : The product of three fractional numbers remains the same in whatever order they are grouped for the purpose of multiplication, i.e.,for multiplication is associative.
For example:
Property 5 : Multiplication of fractional numbers is distributed over addition and subtraction of fractional numbers,i.e.,
For example :
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise-6E Nos 1-4( a to e ) pages-57-58 and Exercise-6F Nos 1-5 pages 59-60 in ex-bk.
09 / 07 / 2021
Ch:6 Fractional Numbers
Page nos:- 55 and 56
Ch:6 Fractional Numbers
Page nos:- 55 and 56
Multiplication of Fractions
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise- 6C Nos 2,4,6,8,10,12,14,16,18,20,22,24,26 and do Exercise-6D Nos 1,3,5,7,9,11,13,15 and 17 in ex-bk.
06 / 07 / 2021
Ch:6 Fractional Numbers
Page no:- 53
Addition of Fractions
Method : To add two or more fractions,we first change all the fractions to their equivalent fractions with common denominators .This common denominator is the LCM of the denominators of the given fractions. Now add these like fractions. After addition convert it into a mixed fraction. Always give the answer in its simplest form.
Example:
Now watch the video to help you understand better.
ASSIGNMENTS
Do Exercise- 6B Nos 1,3,5,7,9,11,13,15,17,19,21,23,25 and 27 page nos-53-54 in ex-bk.
02 / 07 / 2021
Ch: 6 Fractional Numbers
Page nos:- 49-51
Conversions of Mixed numbers into Improper Fraction
Conversion of Improper Fractions to a Mixed Numbers
Comparison of Fractions
Comparison of Fractions with Unlike Numerators and Unlike Denominators
Method: We compare the fractions with unlike numerators and unlike denominators by changing them into fractions having the same denominator (like fractions) by taking the L.C.M. of denominators.
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-6 ( A ) Nos 8 to 15 page nos- 52 and 53 in ex-bk.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
18 / 06 / 2021
Ch: 6 Fractional Number
Download Ch:6 in pdf by clicking on the chapter's name above.
Page nos:- 46-48
Ch: 6 Fractional Number
Download Ch:6 in pdf by clicking on the chapter's name above.
Page nos:- 46-48
Now watch the videos to help you understand better.
ASSIGNMENT
Do Exercise- 6A Nos 1-7 (a,b,c,d) page nos 51-52 in ex-bk.
15 / 06 / 2021
Chapter- 5 H.C.F. and L.C.M.
Page nos:- 40-44
Page nos:- 40-44
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise- 5B Nos 1,3,5,7,9,11,13,15,17,19,21 and 23 page no 42 and Exercise-5C Nos 1-10 page nos 43-44 in ex-bk.
Do Exercise- 5B Nos 1,3,5,7,9,11,13,15,17,19,21 and 23 page no 42 and Exercise-5C Nos 1-10 page nos 43-44 in ex-bk.
11 / 06 / 2021
REVISION
Chapter- 1 Large Numbers
Chapter- 2 Addition and Subtraction
ASSIGNMENTS
Revise Chapters 1 and 2 all ex's.
08 / 06 / 2021
(Download Ch-5 in pdf by clicking on the chapter's name above.)
HIGHEST COMMON FACTOR (H.C.F.) OR GREATEST COMMON FACTOR (G.C.F.)
The H.C.F. or G.C.F. of two or more numbers is the greatest number which is a factor of both or all the numbers.
There are 3 methods to calculate the HCF of two numbers:
There are 3 methods to calculate the HCF of two numbers:
- HCF by listing out the common factors
- HCF by prime factorization
- HCF by division method
H.C.F. by Listing out the Common Factors
In this method, we list out the factors of each number and determine the common factors of those numbers. Then, among the common factors, we determine the highest common factor. Let's understand this method using an example.
We will find the HCF of 30 and42. We will list the factors of 30 and 42. The factors of 30 are1, 2, 3, 5, 6, 10, 15, and 30 and the factors of 42 are1, 2, 3, 6, 7, 14, 21, and 42. Clearly, 1, 2, 3, and 6 are the common factors of 30 and 42. But, 6 is the common factor and the greatest one. Hence, the HCF of 30 and 42 is 6.
H.C.F. by Prime Factorisation
In this method, we find the prime factorisation of each number and find the common prime factors of those numbers. Then, we find the HCF of those numbers by finding the product of the prime factors that are common to each of the given numbers. Let's understand this method using an example.
In this method, we find the prime factorisation of each number and find the common prime factors of those numbers. Then, we find the HCF of those numbers by finding the product of the prime factors that are common to each of the given numbers. Let's understand this method using an example.
We will find the HCF of 60 and 90. Let's represent the numbers using the prime factorization.So, we have, 60 = 2 × 2 × 3 × 5 and 90 = 2 × 3 × 3 × 5. Now, HCF of 60 and 90 will the product of common prime factors, that are, 2, 3, and 5. So, HCF of 60 and 90 =2 × 3× 5 = 30.
H.C.F. by Division Method
In this method, we divide the larger number by the smaller number and check the remainder. Then, we make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform the long division again. We continue the long division process till we get the remainder as 0 and the last divisor will be the HCF of those two numbers.Let's understand this method using an example.
In this method, we divide the larger number by the smaller number and check the remainder. Then, we make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform the long division again. We continue the long division process till we get the remainder as 0 and the last divisor will be the HCF of those two numbers.Let's understand this method using an example.
Now watch the videos to help you understand better.
Video-3 H.C.F. by Long Division Method
ASSIGNMENTS
Do Exercise- 5A Nos 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,38,41,43,45,47 and 49 page nos 39-40 in ex-bk.
04 / 06 / 2021
Ch- 3 Multiplication and Division
Page nos:- 28 and 29
WORD PROBLEM ON DIVISION
Example:- If 9975 kg of wheat is packed in 95 bags, how much wheat will each bag contain?
Solution:
Since 95 bags contain wheat 9975 kg
Therefore, 1 bag contains wheat (9975 ÷ 95) kg
= 105 kg
(Download Ch-4 in pdf by clicking on the chapter's name above.)
Page nos:- 31-35
The numbers which are divisible by 2 are called even numbers.
Hence, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ....... etc are even numbers.
The numbers which are not divisible by 2 are called odd numbers. So, odd number is always 1 more than an even number.
Thus, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23 ....... etc are odd numbers.
Prime Numbers:
Prime numbers are those numbers which have only two factors 1 and the number itself.
In other words, a number which is divisible by only itself and 1 is a prime number. So, prime number has only two different factors 1 and the number itself.
For example, these numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, etc which have only two factors i.e. 1 and the number itself.
Twin Primes:
If the difference between the two prime numbers is 2 they are called twin primes. For example (3, 5), (5, 7) and (11, 13) are set of twin primes. So, two consecutive prime numbers having only one number between them are called twin primes.
Co-Prime Numbers:
If two numbers have only 1 as a common factor, they are called as co-primes. For example (2, 3), (4, 5), (3, 7) and (4, 9) are co-primes.
Composite Numbers:
Composite numbers are those numbers which have more than two factors.
In other words, a number that has more than two different factors is a composite number. So, a composite number is also exactly divisible by numbers other than 1 and itself.For example, 4 is a composite number and it can be divided by 1, 2 and 4.
Properties of Factors
- Every non-zero number is a factor of itself.
Examples: 5 is a factor of 5. (5 ÷ 5 = 1)
12 is a factor of 12. (12 ÷ 12 = 1) - 1 is a factor of every number.
Examples: 1 is a factor of 5. (5 ÷ 1 = 5)
1 is a factor of 12. (12 ÷ 1 = 12) - Every non-zero number is a factor of 0.
Example: 5 and 12 are factors of 0 because
0 ÷ 5 = 0 and 0 ÷ 12 = 0 - The factors of a number are finite.
Multiples
Multiple: A multiple of any natural number is a number formed by multiplying it by another natural number.
Example: Multiples of 6 are 6 × 1 = 6; 6 × 2 = 12; 6 × 3 = 18; 6 × 4 = 24
Here, 6,12,18,24 are multiples of 6.
Properties of Multiples
- Every number is a multiple of itself.
Examples
(a) 3 × 1 = 3; 3 is the multiple of 3
(b) 7 × 1 = 7; 7 is the multiple of 7 - Every number is the multiple of 1.
Examples
(a) 1 × 3 = 3; 3 is the multiple of 1
(b) 1 × 7 = 7; 7 is the multiple of 1 - The multiples of a number are infinite (unlimited)
Prime factorization of any number means to represent that number as a product of prime numbers. For example, prime factorization of 40 is the representation of 40 as a product of prime numbers and can be done in the following way:
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-3E Nos 1,3,5,7,9 and 10 page no 29 and Exercise-4A full page nos 35-36 in ex-bk.
01 / 06 / 2021
Ch- 3 Multiplication and Division
Page no:- 24
WORD PROBLEM ON MULTIPLICATION
A carton holds 24 packets of biscuits. Each packet has 12 biscuits. How many biscuits can be packed in 45 cartons?
In one carton we can pack 24 × 12 biscuits.
In 45 cartons, we can pack 24 × 12 × 45 biscuits.
24 × 12 = 288
Therefore, altogether there are 12,960 biscuits
Page nos:-25-28
Dividend:The dividend is the number that is being divided in the division process.
Divisor:The number by which dividend is being divided by is called divisor.
Quotient: A quotient is a result obtained in the division process.
Remainder:The remainder is the portion of the dividend that is left over after division.
An important result: Dividend = (Divisor × Quotient) + Remainder
Example : Divide 470988 by 378
For example in the above figure, the dividend is 470988, the divisor is 378 and the quotient is 1246 and the remainder is 0.
Check : Divisor × Quotient + Remainder = Dividend
378 × 1246 + 0 = 470988
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-3C Nos 1,2,3,5,7,9 and 11 page no 25 and Exercise-3D Nos 1,3,5,7,9,11,13,15,17,19,21,23,25 and 27 page no 28 in ex-bk.
28 / 05 / 2021
Ch- 3 Multiplication and Division
(Download Ch- 3 in pdf by clicking on the chapter's name above.)
Page nos:- 21-23
(Download Ch- 3 in pdf by clicking on the chapter's name above.)
Page nos:- 21-23
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-3A full page no 22 in ex-bk and do Exercise-3B Nos 2,4,6,8,10,12,14,16,18,20,22,24, 26,28,30 and 32 page no 24 in ex-bk.
25 / 05 / 2021
Chapter- 2 Addition and Subtraction
Page nos:-15-19
Chapter- 2 Addition and Subtraction
Page nos:-15-19
Now watch the videos to help you understand better.
ASSIGNMENTS
Do Exercise-2C Nos 1-12 in text book + Nos 13,15,17,19,21,23 and 25 in ex-bk page nos 17-18 and do Exercise-2D Nos 1,3,5,7,9,11,13,15 and 16 page nos 19-20 in ex-bk.
Do Exercise-2C Nos 1-12 in text book + Nos 13,15,17,19,21,23 and 25 in ex-bk page nos 17-18 and do Exercise-2D Nos 1,3,5,7,9,11,13,15 and 16 page nos 19-20 in ex-bk.
21 / 05 / 2021
Chapter- 2 Addition and Subtraction
(Download Ch-2 in pdf by clicking on the chapter's name above.)
Page nos:- 10-14
(Download Ch-2 in pdf by clicking on the chapter's name above.)
Page nos:- 10-14
Now watch the videos to help you understand better.
ASSIGNMENTSDo Exercises (2A and 2B) full page nos-13 and 14 in ex-bk.
18 / 05 / 2021
Ch-1 Large Numbers
Page no-8
INTERNATIONAL OR WESTERN SYSTEM OF WRITING NUMBERS IN WORDS
Page no-8
INTERNATIONAL OR WESTERN SYSTEM OF WRITING NUMBERS IN WORDS
The system of writing numbers in words discussed earlier is called Indian System. In International System, We use the following:
1 lakh = 100 thousands
10 lakh = 1 million
1 crore = 10 millions
10 crores = 100 millions
The 1st period consists of ---> ones, tens and hundred.
The 2nd period consists of ---> thousand, 10 thousand and 100 thousands.
The 3rd period consists of ---> million, 10 million and 100 million.
What is the difference between the Indian and International numeral system?
The main difference between the Indian and International numeral system is the placement of commas (separator). In the Indian system, lakhs are written after thousands, whereas in the International system, millions are written after thousands.
The main difference between the Indian and International numeral system is the placement of commas (separator). In the Indian system, lakhs are written after thousands, whereas in the International system, millions are written after thousands.
Example : The number 50,801,592 is read as fifty million, eight hundred and one thousand, five hundred and ninety two.
Now watch this video to help you understand better.
Video-1 International System of Numeration
ASSIGNMENTS
Do Exercise-1C Nos 1 and 2 page nos- 8 and 9.
Do Exercise-1C Nos 1 and 2 page nos- 8 and 9.
11 / 05 / 2021
Ch-1 Large Numbers
Page nos :- 6 and 7
ORDER RELATION
Page nos :- 6 and 7
ORDER RELATION
We have already learnt the method of finding the greater of the two 4-digit numbers. Here we shall learn the method of finding the greater of the two 5-digit numbers or 6-digit numbers or more digit numbers with the help of following two rules
Rule I: We know that a number with more digits is always greater than the number with less number of digits.
Example: Which is greater?
60,36,15,589 or 8,59,76,456
Solution:
60,36,15,589 or 8,59,76,456
The number 60,36,15,589 has 9-digits and 8,59,76,456 has 8-digits.
Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits.
Example:
Compare 69,56,16,430 and 69,37,82,890
Solution:
Both numbers have same numbers of digits.
Let us compare the digits in the left most place, we find the both numbers have same digits in ten-crores and crores place. Next, we compare the digits at ten-lakhs place. Here 5 > 3.
Thus, 69,56,16,430 > 69,37,82,890.
ASCENDING AND DESCENDING ORDER
We know, while arranging numbers from the smallest number to the largest number, then the numbers are arranged in ascending order.
Suppose for example, 81, 97, 123, 137 and 201 are arranged in ascending order.
Vice-versa while arranging numbers from the largest number to the smallest number then the numbers are arranged in descending order.
Suppose for example, 187, 121, 117, 103 and 99 are arranged in descending order.
Now watch these videos to help you understand better.
Video-2 Ascending and Descending Order
ASSIGNMENTS
Do Exercise-1B Nos 1-3 page nos- 7 and 8.
Do Exercise-1B Nos 1-3 page nos- 7 and 8.
04 / 05 / 2021
Ch-1 Large Numbers
(Download Ch-1 in pdf by clicking on the chapter name above.)
Page nos :- 1-3
NUMBERS UPTO TEN - LAKHS
(Download Ch-1 in pdf by clicking on the chapter name above.)
Page nos :- 1-3
NUMBERS UPTO TEN - LAKHS
Numeral of a Number : The group of figures representing a number is called the numeral of that number.
The numeral for the number eight thousand seven hundred sixty five is 8765. It is the group of figures (5,6,7 and 8) which represent the given number.
In class IV, you have studied numbers upto 6-digits. The largest 6-digit number is 9,99,999. Let us see what is the number ' 1 more than 9,99,999 '.
9.99,999 +1 = 9,00,000 +90,000 +9,000+ 900 +90+9+1
= 9,00,000+90,000+9,000+900 +90 +10 [Adding ones as: 9+1 = 10]
= 9,00,000+90,000 +9,000 +900+ 100 [Adding tens as: 90 +10 = 100]
= 9,00,000 +90,000 +9,000+ 1000 [Adding hundreds as: 900 +100 = 1,000]
= 9,00,000 +90,000 +10,000[ Adding thousands as: 9,000+ 1,000= 10,000]
= 9,00,000+1,00,000 [Adding ten-thousands as: 90,000+10, 000 = 1,00,000]
=10,00,000. [Adding lakhs as: 9,00,000+1,00,000 = 10,00,000]
10,00,000 stands for ten-lakhs.
The number 10,00,000 has 7-digits. It is the smallest number of 7-digits.
The seventh place from the right is called the ten-lakhs' place.
EXTENDING NUMBERS BEYOND TEN-LAKHS
The greatest 7-digit number is 99,99,999. It is read as ninety nine lakh ninety nine thousand nine hundred ninety-nine. If we add 1 to it, we get 1,00,00,000. We read this number as 1 crore. The number 1,00,00,000 has 8-digits. It is the smallest 8-digit number. The eighth place in the number is called crore's place. The largest 8-digit number is 9,99,99,999. It is read as nine crore ninety nine lakh ninety nine thousand nine hundred and ninety-nine. Indian System of Numeration
Place Value Chart according to the Indian System of Numeration.
In Indian system we start grouping the number from right in group of 3 and further in group of 2.The place value chart have been separated into groups called periods i.e. ones, thousands, lakhs and crores.
Reading of number according to Indian System of Numeration
In Indian System of Numeration periods such as ones, thousands, lakhs, crores, etc. are used so that number can be easily read.
Let’s read the below number according to Indian System of Numeration
11, 54, 08, 453
First put the number in their respective places.
This number is read as eleven crore fifty four lakh eight thousand four hundred fifty three.
Marking periods according to Indian System of Numeration
Different periods like ones, thousands, lakhs and crores are separated by comma (,) starting from the right to differentiate the periods.
We start with the first period, named as ones period, consist the first three digits of the given number. The second period (i.e. thousands period) is consist of the next two digits of the given number. The third period (i.e. lakhs period), consist of the next two digits of the given number. The fourth period (i.e. crores period), consist of the next two digits of the given number.
Let’s differentiate periods by placing commas in between.
Example: 457833228
This number is separated by comma as 45, 78, 33, 228
Now watch this video
ASSIGNMENTS
Study and practice page nos 1-3 and do Exercise-1A Nos 1-5 page no-5 in ex-bk.
